বাইনারি যোগ বিয়োগ Addition and Subtraction in Binary System

বাইনারি সংখ্যা আমাদের পরিচিত দশমিক সংখ্যার মতোই একটি সংখ্যা পদ্ধতি। পার্থক্যটুকু হচ্ছে যে দশমিক সংখ্যা পদ্ধতিতে ভিত্তি 10 এবং বাইনারিতে ভিত্তি 2।

কাজেই দশমিক সংখ্যা পদ্ধতিতে আমরা যেভাবে যোগ এবং বিয়োগ করতে পারি দশমিক পদ্ধতিতেও হুবহু সেভাবে যোগ এবং বিয়োগ করতে পারব।  যেমনঃ- 

তবে যেহেতু বাইনারি সংখ্যার সবচেয়ে বড় ব্যবহার ডিজিটাল ইলেকট্রনিক্সে তাই বাইনারি যোগ এবং বিয়োগের প্রয়োগের জন্য আলাদা কিছু পদ্ধতি ব্যবহার করা হয়। সাধারণ সংখ্যা যোগ-বিয়োগের বেলায় আমাদের কখনোই আমরা কত অঙ্কের সংখ্যা যোগ কিংবা বিয়োগ করছি সেটি আগে থেকে জানার প্রয়োজন হয় না কিন্তু ইলেকট্রনিক সার্কিট ব্যবহার করে বাইনারি যোগ-বিয়োগ করার সময় কত অঙ্কের সংখ্যা যোগ করছি আগে থেকে জানতে হয়। কারণ সার্কিটটি যতগুলো বিট ধারণ করতে পারবে সংখ্যাটিতে তার থেকে বেশি সংখ্যক অঙ্ক থাকলে সেটি ব্যবহার করা যায় না। শুধু তাই নয় যোগ করার পর বিটের নির্ধারিত সংখ্যা থেকে বিটের সংখ্যা বেড়ে গেলে সেটিও সঠিকভাবে ফলাফল দেবে না। ডিজিটাল ইলেকট্রনিক্সে যেহেতু দুটি ভিন্ন ভিন্ন ভোল্টেজ দিয়ে বাইনারি 0 এবং 1 অঙ্ক দুটি দিয়ে প্রকাশ করা হয় তাই যাবতীয় গাণিতিক অঙ্কও এই অঙ্ক দুটো দিয়েই প্রকাশ করতে হবে।

অনেকে মনে করতে পারে ডিজিটাল ইলেকট্রনিক্স করার জন্য বাইনারি সংখ্যা দিয়ে যোগ, বিয়োগ, গুণ এবং ভাগ এই প্রত্যেকটি প্রক্রিয়াই করার ব্যবস্থা থাকতে হয়। আসলে একটি সংখ্যাকে নেগেটিভ করা এবং যোগ করার সার্কিট থাকলেই অন্য সব গাণিতিক প্রক্রিয়া করা যায়। কোনো একটি সংখ্যা বিয়োগ করতে হলে সংখ্যাটিকে নিগেটিভ করে যোগ করতে হবে। সংখ্যা দিয়ে গুণ করার পরিবর্তে সেই নির্দিষ্ট সংখ্যক বার যোগ করলেই হয়। বার বার বিয়োগ করে ভাগের কাজ চালিয়ে নেয়া যায়। তাই আমরা দেখব একটি সংখ্যাকে নেগেটিভ করার একটি সুনির্দিষ্ট পদ্ধতি জানা থাকলে শুধু যোগ করার সার্কিট দিয়ে আমরা বিয়োগ, গুণ, এবং ভাগও করতে পারব।

চিহ্নযুক্ত সংখ্যা Signed Numbers

একটি বাইনারি সংখ্যাকে পজেটিভ বা নেগেটিভ হিসেবে দেখানোর একটি সহজ উপায় হচ্ছে MSB টিকে সাইনের জন্য নির্ধারিত করে রাখা। যদি সেটি ০ হয় তাহলে বুঝতে হবে সংখ্যাটি পজেটিভ আর যদি সেটি 1 হয় তাহলে বুঝতে হবে সংখ্যাটি নেগেটিভ। কাজেই ৪ (আট) বিটের একটি সংখ্যার জন্যে 7টি বিট দিয়ে সংখ্যার মান প্রকাশ করা হবে এবং অষ্টম বিটটি সংখ্যার সাইন প্রকাশ করার জন্য আলাদাভাবে সংরক্ষিত থাকবে। এভাবে সংখ্যা প্রকাশ করার সময় আরো একটি বিষয় সবসময় মেনে চলতে হয়। সংখ্যাগুলোর বিট সংখ্যা সবচেয়ে পরিপূর্ণ রাখতে হবে -এর মাঝে ফাঁকা অংশ থাকতে পারবে না। আট বিটের সংখ্যায় +1 লেখার সময় 01 লেখা যাবে না, 0000001 লিখতে হবে। প্রথম ০টি বোঝাচ্ছে সংখ্যাটি পজেটিভ, পরের সাত বিট দিয়ে 1 লেখা হয়েছে। একইভাবে 1 লিখতে হলে 11 লেখা যাবে না 10000001 লিখতে হবে। প্রথম 1টি বোঝাচ্ছে সংখ্যাটি নেগেটিভ পরের সাতটি বিট দিয়ে সংখ্যার মান (1) প্রকাশ করা হয়েছে। এই পদ্ধতিতে কিছু পজিটিভ এবং নিগেটিভ সংখ্যা লিখে দেখানো হলোঃ

এই পদ্ধতিতে সংখ্যাকে পজেটিভ এবং নেগেটিভ হিসেবে প্রকাশ করায় একটি গুরুতর সমস্যা আছে। সমস্যাটি বোঝার জন্য আমরা নিচে চার বিটের দুটি সংখ্যা লিখছি, এক বিট সাইনের জন্য, বাকি তিন বিট মূল সংখ্যাটির মান বোঝানোর জন্যঃ 0000 এবং 1000

বোঝাই যাচ্ছে প্রথম সংখ্যাটি +0 এবং দ্বিতীয়টি -0 কিন্তু আমরা সবাই জানি, শূন্য (0) সংখ্যাটির পজেটিভ এবং নেগেটিভ হয় না- কিন্তু এই পদ্ধতিতে +0 এবং -0 মেনে নেয়া ছাড়া কোনো উপায় নেই। +0 এবং -0 এর অস্তিত্বটি কম্পিউটারে জটিল হিসেবে অনেক বড় সমস্যার সৃষ্টি করতে পারে।

২-এর পরিপূরক 2's Complement

সাইন বিট দিয়ে সংখ্যার পজেটিভ এবং নেগেটিভ প্রকাশ করার জটিলতা থেকে রক্ষা পাওয়ার একটি চমৎকার পদ্ধতি রয়েছে। সেটি হচ্ছে 2 -এর পরিপূরক (2's complement) বিষয়টি বোঝার আগে আমরা নেগেটিভ সংখ্যা বলতে কী বোঝাই সেটি বুঝে নেই। একটি সংখ্যার সাথে যে সংখ্যাটি যোগ করলে যোগফল শূন্য হবে সেটিই হচ্ছে তার নেগেটিভ সংখ্যা। কাজেই আমাদেরকে কোনো একটি বাইনারি সংখ্যা দেওয়া হলে আমরা এমন আরেকটি বাইনারি সংখ্যা খুঁজে বের করব, যেটি যোগ করলে যোগফল হবে শূন্য।

আমরা আট বিটের একটি বাইনারি সংখ্যা দিয়ে শুরু করি। ধরা যাক সংখ্যাটি 10110011। এবারে আমরা সংখ্যাটির 1 -এর পরিপূরক (1's complement) নিই অর্থাৎ প্রত্যেকটি 1 কে 0 দিয়ে এবং ০ কে 1 দিয়ে পরিবর্তন করে নিইঃ

এই বাইনারি সংখ্যাটি হচ্ছে আট বিটের সর্বোচ্চ সংখ্যা। এর সাথে 1 যোগ করা হলে সংখ্যাটি আর আট বিটে সীমাবদ্ধ থাকবে না, এটি হবে ও বিটের একটি সংখ্যা।

আমরা যেহেতু ৪ (আট) বিটের সংখ্যার মাঝে সীমাবদ্ধ থাকতে চাই, তাই নবম বিটকে উপেক্ষা করে আমরা বলতে পারি সংখ্যাটি ০০০০০০০০ বা শূন্য। যেহেতু একটা সংখ্যার সাথে শুধু তার নেগেটিভ সংখ্যা যোগ করা হলেই যোগফল হিসেবে আমরা শূন্য পাই, তাই আমরা বলতে পারি যে কোনো বাইনারি সংখ্যার 1 কে ০ এবং ০ কে 1 দিয়ে পরিবর্তন করে (বা 1 এর পরিপূরক নিয়ে) যে সংখ্যা পাব তার সাথে 1 যোগ করে নেয়া হলে সেটি মূল বাইনারি সংখ্যার নেগেটিভ হিসেবে কাজ করবে। এই ধরণের সংখ্যাকে বলা হয় মূল সংখ্যাটির ২-এর পরিপূরক।

আমরা এখন 10110011 -এর নিগেটিভ অথবা 2 -এর পরিপূরক বের করতে পারিঃ

কাজেই আমরা বলতে পারি, আট বিটের একটি সংখ্যা হিসেবে 01001101 হচ্ছে 10110011 এর নেগেটিভ। একটি সংখ্যাকে একবার নেগেটিভ করে আবার সেটিকে নেগেটিভ করা হয় তাহলে আমরা আগের সংখ্যাটি ফিরে পাব। আমরা আমাদের এই উদাহরণটিতে সেটি পরীক্ষা করে দেখতে পারি। 01001101কে আবার 2- এর পরিপূরক করা হলে আমরা পাবঃ

আমরা সত্যি সত্যি মূল সংখ্যাটি ফিরে পেয়েছি, অর্থাৎ 01001101 এবং 10110011 হচ্ছে একটি আরেকটির নেগেটিভ।

এবারে একটা খুবই গুরুত্বপূর্ণ বিষয় আমাদের বিবেচনা করতে হবে। আমরা 2 -এর পরিপূরক বের করে যে কোনো বাইনারি সংখ্যাকে তার নেগেটিভ করতে পারব, কিন্তু মূল বাইনারি সংখ্যাটি শুরুতে কত ছিল সেটি কি আমরা জানি? যেমন ধরা যাক 1001 একটি চার বিটের বাইনারি সংখ্যা (যার দশমিক মান হচ্ছে 9), খুব সহজেই আমরা দেখাতে পারি 0111 হচ্ছে এর 2 -এর পরিপূরক (যার দশমিক মান হচ্ছে 7)। অর্থাৎ এই সংখ্যাদুটি একে অপরের 2 -এর পরিপূরকঃ

তাহলে আমরা প্রশ্ন করতে পারি, চার বিটের একটি সংখ্যা হিসেবে আমরা কি 1001 কে +9 ধরে নিয়ে এর 2 -এর পরিপূরক হিসেবে 0111কে -9 ধরে নেব? নাকি 0111কে +7 ধরে নিয়ে 2এর পরিপূরক হিসেবে 1001কে -7 ধরে নেব? এই বিভ্রান্তি থেকে মুক্তি পাবার জন্য একটি নিয়ম মেনে চলা হয়। নিয়মটি হচ্ছে MSB যদি 0 হয় শুধু তাহলেই সংখ্যাটি পজেটিভ হবে এবং বাইনারি সংখ্যাটি প্রকৃত মান দেখাবে। MSB যদি 1 হয় তাহলে সংখ্যাটি নেগেটিভ এবং শুধু ২-এর পরিপূরক নিয়ে তার প্রকৃত পজেটিভ মান বের করা যাবে।

এই পদ্ধতিতে কিছু সংখ্যার নেগেটিভ রূপ বের করে দেখানো হলোঃ

ধন্যবাদ আজকের আর্টিকেলটি পড়ার জন্য। 

আরো পড়ুন

সংখ্যা পদ্বতির প্রকারভেদ

সংখ্যা পদ্ধতি আবিষ্কারের ইতিহাস

বিস্তারিত পড়ুন

সংখ্যা পদ্ধতি আবিষ্কারের ইতিহাস | History of Number System

আমাদের দৈনন্দিন জীবনে আমরা প্রতিনিয়ত ভাষা এবং একই সাথে সংখ্যাকেও ব্যবহার করি। আমাদের প্রয়োজনের কারণে ভাষার সাথে সাথে আমরা সংখ্যা পদ্ধতি আবিষ্কার করেছি। সত্যি কথা বলতে কী অনেক প্রাণী এবং পাখিও অল্প কিছু গুণতে পারে। শুনে অবাক হয়ে যেতে হয় যে এখনো পৃথিবীর গহিন অরণ্যে এমন আদিবাসী মানুষ আছে যাদের জীবনে সংখ্যার বিশেষ প্রয়োজন হয় না বলে সেভাবে গুনতে পারে না। ব্রাজিলের পিরাহা নামের আদিবাসীরা এক এবং দুই থেকে বেশি গুনতে পারে না। এর চাইতে বেশি যে কোনো সংখ্যা হলেই তারা বলে 'অনেক'।

সংখ্যা পদ্ধতি কি, বাইনারি সংখ্যা পদ্ধতি কি, পজিশনাল সংখ্যা পদ্ধতি কি, সংখ্যা পদ্ধতি কাকে বলে, সংখ্যা পদ্ধতির বেজ কি, সংখ্যা পদ্ধতি, হেক্সাডেসিমেল সংখ্যা পদ্ধতি কি, ৩ ভিত্তিক সংখ্যা পদ্ধতি ব্যাখ্যা কর, দশমিক সংখ্যা পদ্ধতি কি, সংখ্যাপদ্ধতি, নন পজিশনাল সংখ্যা পদ্ধতি কি, সংখ্যা পদ্ধতির বেস কি

সংখ্যা পদ্ধতির ইতিহাস

আদিম মানুষ যখন শিকারী হিসেবে বনে-জঙ্গলে ঘুরে বেড়াত তখন হিসেব রাখা বা গোনার সেরকম প্রয়োজন ছিল না। যখন তারা কৃষিকাজ করার জন্য স্থিতু হয়েছে, গবাদি পশু পালন করতে শুরু করেছে, শস্যক্ষেত্রে চাষাবাদ করেছে, গ্রাম, নগর-বন্দর গড়ে তুলেছে, রাজস্ব আদায় করা শুরু করেছে তখন থেকে গোনার প্রয়োজন শুরু হয়েছে। সেজন্য সংখ্যা পদ্ধতির ইতিহাস এবং সভ্যতার ইতিহাস খুবই ঘনিষ্ঠভাবে সম্পর্কিত। আমাদের প্রয়োজনের কারণে এখন আমরা অনেক বড় বড় সংখ্যা ব্যবহার করতে পারি, গণিতের সাহায্যে সেগুলো নানাভাবে প্রক্রিয়া করতে পারি।

আদিম কালে মানুষেরা গাছের ডাল বা হাড়ে দাগ কেটে কিংবা কড়ি, শামুক বা নুড়ি পাথর সংগ্রহ করে সংখ্যার হিসাব রেখেছে। তবে যখন আরো বড় সংখ্যা আরো বেশি স্থায়ীভাবে সংরক্ষণ করার প্রয়োজন হয়েছে তখন সংখ্যার একটি লিখিত রূপ বা চিহ্ন সৃষ্টি করে নিয়েছে। প্রায় পাঁচ হাজার বছর আগে মোটামুটি একই সময়ে সুমেরিয়ান-ব্যবলিয়ান এবং মিশরীয় সভ্যতার শুরু হয় এবং এই দুই জায়গাতেই সংখ্যার প্রথম লিখিত রূপ পাওয়া গেছে।

সংখ্যা পদ্ধতি

সুমেরিয়ান ব্যবলিয়ান সংখ্যা ছিল ষাটভিত্তিক এবং মিশরীয় সংখ্যা ছিল দশভিত্তিক। ব্যবলিয়ান সংখ্যা পদ্ধতির রেশ পৃথিবীতে এখনো রয়ে গেছে, আমরা মিনিট এবং ঘণ্টার হিসেব করি ষাট দিয়ে এবং কোণের পরিমাপ করি ষাটের গুণিতক দিয়ে। সুমেরিয়ান ব্যবলিয়ান সংখ্যা পদ্ধতিতে স্থানীয় মান ছিল, মিশরীয় সংখ্যা পদ্ধতিতে ছিল না। দুই পদ্ধতিতেই কোনো কিছু না থাকলে সেটি বোঝানোর জন্য চিহ্ন ব্যবহার করা হতো কিন্তু সেটি মোটেও গাণিতিক সংখ্যা শূন্য ছিল না।

পরবর্তীকালে আরো তিনটি সভ্যতার সাথে সাথে সংখ্যা পদ্ধতি গড়ে উঠে, সেগুলো হচ্ছে মায়ান সভ্যতা, চীন সভ্যতা এবং ভারতীয় সভ্যতা। মায়ান সংখ্যা পদ্ধতি ছিল কুড়িভিত্তিক, চীন এবং ভারতীয় সংখ্যা পদ্ধতি ছিল দশভিত্তিক। (আমাদের দেশে যেসব মানুষ লেখাপড়ার সুযোগ পায়নি তারা কাজ চালানোর জন্য মৌখিকভাবে কুড়িভিত্তিক এক ধরনের সংখ্যা ব্যবহার করে থাকে।) মায়ান এবং ভারতীয় সংখ্যা পদ্ধতিতে স্থানীয় মান ব্যবহার করে।

প্রয়োজনের কারণে সব সংখ্যা পদ্ধতিতেই শূন্যের জন্য একটি চিহ্ন থাকলেও প্রকৃত অর্থে শূন্যকে একটি সংখ্যা হিসেবে ধরে সেটিকে সংখ্যা পদ্ধতিতে নিয়ে এসে গণিতে ব্যবহার করে ভারতীয়রা এবং এই শূন্য আবিষ্কারকে আধুনিক গণিতের একটি অন্যতম যুগান্তকারী আবিষ্কার হিসেবে বিবেচনা করা হয়। মায়ান এবং চীন সংখ্যা পদ্ধতি মাত্র দুই-তিনটি চিহ্ন ব্যবহার করে লেখা হতো। কিন্তু হাতে লেখার সময় পাশাপাশি অসংখ্য চিহ্ন বসানোর বিড়ম্বনা থেকে বাঁচার জন্য ভারতীয় সংখ্যা পদ্ধতিতে 1 থেকে 9 পর্যন্ত নয়টি এবং শূন্যের জন্য একটি চিহ্ন- এভাবে দশটি চিহ্ন ব্যবহার করতে শুরু করে। আমরা এই চিহ্নগুলোকে অঙ্ক বা Digit বলি।

সংখ্যা পদ্ধতি নিয়ে বিস্তারিত

2500 বছর আগে গ্রিকরা ব্যবলিয়ান এবং মিশরীয়দের সংখ্যা পদ্ধতির উপর ভিত্তি করে তাদের পূর্ণাঙ্গ 10 ভিত্তিক সংখ্যা পদ্ধতি গড়ে তুলেছিল। রোমানরা গ্রিক সভ্যতার পতন ঘটানোর পর গণিতের অভূতপূর্ব বিকাশ থেমে যায়। রোমান সাম্রাজ্যে গণিতের সেরকম প্রয়োজন ছিল না। তাদের সংখ্যাগুলোতে আলাদা রূপ ছিল না এবং রোমান অক্ষর দিয়ে সেগুলো প্রকাশ করা হতো। অনাবশ্যকভাবে জটিল এবং অবৈজ্ঞানিক রোমান সংখ্যা এখনো বেঁচে আছে এবং ঘড়ির ডায়াল বা অন্যান্য জায়গায় মাঝে মাঝে আমরা তার ব্যবহার দেখতে পাই।

Add Mr. AnTor Ali to your Google News feed. 

ইসলামি সভ্যতার বিকাশ হওয়ার পর ভারতীয় সংখ্যা পদ্ধতি আরবদের মাধ্যমে ইউরোপে ছড়িয়ে পড়ে, যেটি আমাদের আধুনিক দশমিক সংখ্যা পদ্ধতি। এখানে উল্লেখ্য যে শূন্য ব্যবহারের ফলে সংখ্যা পদ্ধতিতে বিস্ময়কর অগ্রগতি হলেও খ্রিষ্টীয় শাসকেরা শূন্যকে শয়তানের রূপ বিবেচনা করায় দীর্ঘদিন সেটাকে ঠেকিয়ে রাখার চেষ্টা করেছিল!

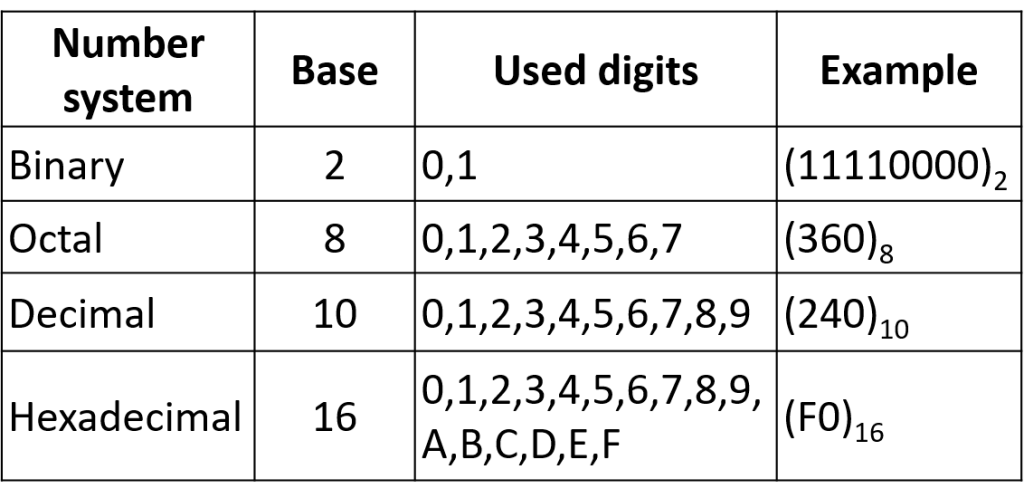
আমাদের হাতে দশ আঙুল থাকার কারণে দশভিত্তিক সংখ্যা গড়ে উঠলেও দুই, আট কিংবা ষোলোভিত্তিক সংখ্যাও আধুনিক প্রযুক্তিতে ব্যাপকভাবে ব্যবহার করা হয়।

সংখ্যা পদ্ধতি (Number System)

সংখ্যাকে প্রকাশ করার এবং গণনা করার পদ্ধতিকে সংখ্যা পদ্ধতি বলে। সংখ্যাকে প্রকাশ করার জন্য বিভিন্ন প্রতীক বা চিহ্ন ব্যবহার করা হয়। এই প্রতীকগুলোকে দুটো ভিন্ন ভিন্ন পদ্ধতিতে ব্যবহার করা যায়।

সংখ্যা পদ্ধতি কি, বাইনারি সংখ্যা পদ্ধতি কি, পজিশনাল সংখ্যা পদ্ধতি কি, সংখ্যা পদ্ধতি কাকে বলে, সংখ্যা পদ্ধতির বেজ কি, সংখ্যা পদ্ধতি, হেক্সাডেসিমেল সংখ্যা পদ্ধতি কি, ৩ ভিত্তিক সংখ্যা পদ্ধতি ব্যাখ্যা কর, দশমিক সংখ্যা পদ্ধতি কি, সংখ্যাপদ্ধতি, নন পজিশনাল সংখ্যা পদ্ধতি কি, সংখ্যা পদ্ধতির বেস কি

বিস্তারিত পড়ুন

What is an Information System?

An information system (IS) is a formal, sociotechnical, organizational system designed to collect, process, store, and distribute information. From a sociotechnical perspective, information systems are composed by four components: task, people, structure (or roles), and technology.

Information systems can be defined as an integration of components for collection, storage and processing of data of which the data is used to provide information, contribute to knowledge as well as digital products that facilitate decision making.

Types of Information Systems

There are many different types of information systems, each designed to serve a specific purpose. Some common types of information systems include:

• Transaction processing systems (TPS): TPSs are used to automate routine, repetitive tasks such as processing orders, payroll, and inventory.
• Management information systems (MIS): MISs provide managers with reports and summaries of data from TPSs. MISs can be used to track performance, make decisions, and plan for the future.
• Decision support systems (DSS): DSSs are interactive computer-based systems that help managers make decisions. DSSs use data from TPSs and MISs, as well as other sources, to provide managers with information that can be used to make better decisions.
• Executive information systems (EIS): EISs are designed for senior executives. EISs provide executives with a summarized view of the organization's performance. EISs can be used to track trends, identify problems, and make strategic decisions.
• Expert systems (ES): ESs are computer programs that mimic the reasoning of human experts. ESs can be used to solve problems in a variety of domains, such as medicine, finance, and manufacturing.
• Artificial intelligence (AI): AI is a field of computer science that deals with the creation of intelligent agents, which are systems that can reason, learn, and act autonomously. AI is used in a variety of information systems, such as ESs, natural language processing systems, and image recognition systems.

Benefits of Information Systems

Information systems can provide a number of benefits to organizations, including:

• Increased efficiency: Information systems can help organizations to automate tasks and processes, which can lead to increased efficiency.
• Improved decision-making: Information systems can provide managers with access to data and information that can be used to make better decisions.
• Enhanced customer service: Information systems can help organizations to provide better customer service by providing customers with access to information and services 24/7.
• Increased productivity: Information systems can help organizations to increase productivity by automating tasks and processes.
• Reduced costs: Information systems can help organizations to reduce costs by automating tasks and processes.
• Improved competitive advantage: Information systems can help organizations to gain a competitive advantage by providing them with access to information and resources that their competitors do not have.

Challenges of Information Systems

While information systems can provide a number of benefits, they also pose a number of challenges, including:

• Security: Information systems are vulnerable to security threats, such as hacking, data breaches, and malware.
• Privacy: Information systems collect and store a large amount of data about individuals, which raises privacy concerns.
• Integration: Information systems from different vendors may not be compatible, which can make it difficult to integrate them into a single system.
• Training: Employees need to be trained on how to use information systems effectively.
• Cost: Information systems can be expensive to purchase, implement, and maintain.

Conclusion

Information systems are an essential part of modern organizations. They can provide a number of benefits, such as increased efficiency, improved decision-making, enhanced customer service, increased productivity, reduced costs, and improved competitive advantage. However, information systems also pose a number of challenges, such as security, privacy, integration, training, and cost. Organizations need to carefully consider the benefits and challenges of information systems before implementing them.

বিস্তারিত পড়ুন

সংখ্যা পদ্বতির প্রকারভেদ

আমরা সাধারণত গণনার কার্যাদি সম্পাদনের জন্য ১০ টি অংক ব্যাবহার করে থাকি। যেমনঃ ০, ১, ২, ৩, ৪, ৫, ৬, ৭, ৮, ৯ এই পদ্ধতিকে ডেসিম্যাল পদ্ধতি বলে। আবার কম্পিউটারের সকল কার্যাদি সম্পাদিত হয় ০, ১ এই অংকের মাধ্যমে। গণিতের এই পদ্ধতিকে বাইনারি বলে।

সংখ্যা পদ্ধতি ৪ প্রকার, যথাঃ-

1. ডেসিম্যাল নাম্বার (Decimal Number)
2. বাইনারি নাম্বার (Binary Number)
3. অকটাক নাম্বার (Octal Number)
4. হেক্সাডেসিম্যাল নাম্বর (Hexadecimal Number)

১. দশমিক পদ্ধতি (ডেচিমাল System)

আমরা সচরাচর যে পদ্ধতিতে সংখ্যা লিখে থাকি এতে ১০ টি প্রতিক ব্যাবহার করা হয়। প্রতিক দশটি হলোঃ ০,১,২,৩,৪,৫,৬,৭,৮,৯ এই পদ্ধতিতে গণনার কার্য করে থাকি। দশমিক সংখ্যার পদ্ধতির বেজ ভিত্তি সংখ্যা ১০। সকল পদ্ধতিতেই অংকের অবস্থানের এর মান নির্ভর করে। নিচের ছবিটি লক্ষ করুন।

২. বাইনারি পদ্ধতি (Binary System)

কম্পিউটারে ব্যাবহৃত প্রায় সব প্রোগ্রামগুলিতে দশমিক পদ্ধতিতে উপাত্ত গ্রহণ করে। তবে বিদ্যুতের উপস্থিতি এবং অনুপস্থিতি ছাড়া অন্য কিছু বুঝতে পারে না। এজন্য বাইনারি সংখ্যা নামে একটি সংখ্যা পদ্ধতির প্রচলন শুরু হয়। এই পদ্ধতিতে কম্পিউটারে বিদ্যুতের উপস্থিতিকে ১ এবং অনুপস্থিতিকে ০ ধরা হয়, যা মেশিনের জন্য সহজে বোধ্যগম্য হয়। এজন্য কম্পিউটারের আভ্যন্তরিণ কাজে বাইনারি পদ্ধতি ব্যাবহার হয়। এই পদ্ধতি সবচেয়ে সরলতম সংখ্যা পদ্ধতি; যার বেজ বা ভিত ২। এতে ০ ও ১ এই দুটি মৌলিক সংখ্যা ব্যাবহার করা হয়। তবে এ পদ্ধতির উপস্থাপিত সংখ্যাগুচ্ছ দীর্ঘকৃতির হয়ে থাকে।

৩. অকটাল পদ্ধতি (Octal System)

বাইনারি অংক বেশ দীর্ঘকৃতি। তাই একে সহজে ও ছোট আকারে উপস্থাপনের জন্য অক্টাল সংখ্যা পদ্ধতির উদ্ভব। এই পদ্ধতির বেজ বা ভিত ৮। এখানে ০,১,২,৩,৪,৫,৬,৭ এই আটটি মৌলিক সংখ্যা ব্যাবহার করে গানিতিক হিসাব নিকাশ সম্পাদন করা হয়। এই পদ্ধতির সবচেয়ে বড় সংখ্যা হলো ৭। এই সংখ্যা পদ্ধতিটি কম্পিউটারের অভ্যান্তরিন বাইনারি সংখ্যায় প্রক্রিয়াকরণের কাজে ব্যাবহৃত হয়। 

৪. হেক্সাডেসিম্যাল পদ্ধতি (Hexadecimal System)

হেক্সাডেসিম্যাল পদ্ধতিতে মোট ১৬ টি মৌলিক অংক ব্যাবহৃত হয়। সেগুলো হল ০,১,২,৩,৪,৫,৬,৭,৮,৯, A, B, C, D, E ও F. এই ১৬ টি মৌলিক অংক ব্যাবহার করে সকল প্রকার গানিতিক হিসাব সম্পাদন করা হয়। এই সংখ্যা পদ্ধতির বেজ ১৬। এই পদ্ধতিতে দশমিক পদ্ধতির ১০ এর মান A এবং ১৫ এর মান F, এবং একি ভাবে B মান হলো ১১ ও C এর মান হলো ১২ এইভাবে বাকি মান গুলো নির্ণয় হয়। F এই পদ্ধতির বড় সংখ্যা। ফলে এর চেয়ে বড় সংখ্যা লিখতে হলে একাধীক হেক্সাডেসিমেল অংকের বিন্যাস করে ব্যাবহার করতে হয়। 

বিস্তারিত পড়ুন